Решение транспортных задач линейного программирования
Среди всех задач линейного программирования (ЗЛП) особняком стоят несколько типов, в частности, транспортные задачи. Конечно, и их можно решить общепринятым симплекс-методом, но вычисления получатся неоправданно сложными и объемными из-за размерности задачи (например, для самой простой задачи с 3 складами и 3 поставщиками - 9 ограничений и 9 переменных).
Поэтому для решения транспортных задач были разработаны специальные методы: для нахождения опорного/начального плана (минимального элемента, северо-западного угла, Фогеля), и для нахождения оптимального плана (метод потенциалов, дифференциальных рент, распределительный метод).
Помимо стандартных задач, мы приводим подробное решение транспортной задачи с ограничениями на пропускную способность и транспортную задачу в сетевой постановке.
Примеры решений транспортных задач ЛП некоторыми из этих методов приведены в этом разделе - изучайте, ищите похожие, решайте (также вы можете перейти к примерам решения ТЗ в Excel). Если вам нужна помощь в выполнении подобных заданий, перейдите в раздел: Решение контрольных работ по линейному программированию.
Примеры решения транспортной задачи онлайн
Задача 1. Из трех холодильников Ai, i=1..3, вмещающих мороженную рыбу в количествах ai т, необходимо последнюю доставить в пять магазинов Bj, j=1..5 в количествах bj т. Стоимости перевозки 1т рыбы из холодильника Ai в магазин Bj заданы в виде матрицы Cij, 3x5.
Написать математическую модель задачи и спланировать перевозки так, чтобы их общая стоимость была минимальной.
Задача 2. Построить закрытую модель транспортной задачи.
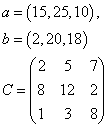
Задача 3. В таблице приведены исходные данные транспортной задачи: заданы удельные транспортные расходы на перевозку единицы груза, слева указаны возможности поставщиков, а сверху – спрос потребителей.
Сформулируйте экономико-математическую модель транспортной задачи, распределительным методом найдите оптимальный план перевозок.
(таблица в файле)
Задача 4. Решить транспортную задачу
1) методом потенциалов (опорный план построить всеми известными способами);
2) методом дифференциальных рент;
3) любым методом при ограничениях: x24≥4, x35≤5, x12=3.
(таблица в файле)
Задача 5. Выполнить решение в программе QM for Windows
Числа в скобках – коэффициенты транспортных расходов, столбец чисел справа от матрицы – запасы груза у поставщиков, строка снизу – потребности потребителей.
1. Решить и проанализировать ТЗ без ограничений.
2. Решить ТЗ с запретом перевозки по самому выгодному пути (с наименьшими затратами).
3. Решить двухэтапную ТЗ с числом поставщиков – 3, складов – 2 и потребителей – 4, взяв за c_ik первых два столбца коэффициентов исходной матрицы, а за c_kj – последние две строки этой матрицы. Мощности складов одинаковы и равны половине суммарных запасов поставщиков, округлённых до целых десятков в большую сторону.
Задача 6. Составить математическую модель транспортной задачи и решить её методом потенциалов.
Завод имеет 3 цеха А, В, С и 4 склада №1,2,3,4. Цех А производит 30 тыс.штук изделий, цех В – 40 тыс. штук изделий, С – 20 тыс. штук изделий. Пропускная способность склада №1 - 20 тыс. штук изделий, №2 - 30 тыс. штук изделий, №3 – 30 тыс.штук, №4 – 10 тыс. штук. Стоимость перевозки из цеха А соответственно в склады №1,2,3,4 1 тыс. штук изделий составляет 20, 30, 3, 4 р., из цеха В 1 тыс. – соответственно 3, 20, 5, 1 р., а из цеха С – соответственно 4, 30, 2, 6 р.
Составить такой план перевозок изделий, при котором расходы на перевозку 90 тыс. изделий были бы наименьшими.
Примеры решения сетевой транспортной задачи
Задача 7. Имеется сеть железных дорог, на которой расположены 3 пункта отправления однородного груза и 9 станций его приема. Известны затраты на перевозку грузов от i-ой до j-ой станции. Заданы объемы ресурсов в каждом пункте отправления и объемы прибытия в каждый пункт назначения. Требуется составить оптимальный план перевозок, предусматривающий минимальные суммарные затраты.
1. Пункты 1, 2, 3 - пункты отправления с объемом запаса, соответственно 200, 150 и 150.
Потребности пунктов назначения таковы: 4 - 40, 5 - 70, 6 - 40, 7 - 50, 8 - 45,9 - 60,10 - 70,11 - 75,12 - 50.
Затраты между соответствующими вершинами заданы: 1-5 - 65, 1-7 - 75, 1-9 - 25, 2-5 - 60, 2-6 - 115, 2-9 - 25, 2-12 - 90, 3-4 - 95, 3-8 - 30, 3-10 - 45, 3-11 - 40, 4-8- 15, 4-12 - 40, 5-7 - 95, 5-9 - 35, 6-8 - 65, 6-9 - 15, 6-11 - 55,6-12 - 80,7-10 - 15,8-11 - 45,9-11 - 35,10-11-110.
2. Пункты 1, 2, 3 - пункты отправления с объемом запаса, соответственно 200,150 и 150.
Потребности пунктов назначения таковы: 4 - 40, 5 - 70, 6 - 40, 7 - 50, 8-45,9-60,10-70,11 -75,12-50.
Затраты между соответствующими вершинами заданы: 1-5 - 65, 1-7 - 75, 1-9 - 25, 2-5 - 60, 2-6 - 115, 2-9 - 25, 2-12 - 90, 3-4 - 95, 3-8 - 30, 3-10 - 45, 3-11 - 40, 4-8 - 15, 4-12 - 40, 5-7 - 95, 5-9 - 35, 6-8 - 65, 6-9 - 15, 6-11 - 55,6-12 - 80,7-10 - 15,8-11 - 45, 9-11 - 35,10-11 -110.
Для следующих звеньев существуют ограничения на пропускные способности. 1-7 - 40, 1-11 - 10, 2-9 - 15, 3-10 - 30.
Задача 8. Пункты производства и потребления связаны между собой транспортной сетью. В пунктах производства сосредоточено некоторое количество однородного груза, которое необходимо вывезти в пункты потребления. Стоимость перевозки единицы груза на каждом участке (равная Сs) задана. Предполагается, что на каждом участке перевозка грузов осуществляется в одном направлении. Требуется составить такой план перевозки, при котором транспортные расходы будут минимальными.




